Roofline 模型详解

Part 1 of How To Scale Your Model (第0部分：导论 | 第2部分：TPU)

跑算法就像开车送货：速度取决于三件事——发动机多快（算力）、路有多宽（带宽）、货仓多大（内存）。Roofline 模型帮我们算出一个操作最快能跑多快、瓶颈在哪里。

时间花在哪了？

先问一个最基本的问题：为什么一个算法跑 50ms 而不是 50s 或者 5ms？模型里到底在干嘛，时间都花在哪了？

要回答这个问题，得先搞清楚三件事：

1. 计算时间

深度学习的核心就是一堆矩阵乘法，每个都由大量浮点加法和乘法组成。这些运算总称为”FLOPs”（Floating-point Operations，浮点运算数）。

计算需要多久？就是运算量除以算力：

\[\begin{equation} T_\text{计算} = \frac{\text{FLOPs 总量}}{\text{芯片每秒能做的 FLOPs}} \end{equation}\]

举个例子：

NVIDIA H100 大约能做 9.89×10¹⁴ bfloat16bf16 是 bfloat16 的缩写，机器学习常用的一种 16 位浮点格式。 FLOPs/s
TPU v6e 大约能做 9.1×10¹⁴ FLOPs/sH100 和 B200 实际只能跑到标称算力的 80-85%，而 TPU 正常能跑到 95%。

所以做 1 万亿次（10¹²）运算，H100 大约要 10¹² / 9.89×10¹⁴ ≈ 1ms。这里没考虑价格差异。

2. 芯片内通信时间

数据存在”显存”（HBM）里，要算的时候得先搬到计算核心。搬运速度取决于内存带宽：

H100 的 HBM 带宽约 3.35TB/s
TPU v6e 约 1.6TB/s

3. 芯片间通信时间

当模型大到一张卡放不下，需要多卡协作时，数据还得在卡之间传来传去。常见的连接方式有 ICI、NVLink、PCIe 等，各有不同的带宽。

通信时间的计算也很简单：数据量除以带宽：

\[\begin{equation} T_\text{通信} = \frac{\text{需要搬运的字节数}}{\text{带宽（字节/秒）}} \end{equation}\]

好消息：计算和通信通常可以重叠进行（一边算一边传）。所以：

运行时间的下界 = 两者的最大值（如果能完美重叠）
运行时间的上界 = 两者之和（如果完全不能重叠）

\[\begin{equation} T_\text{下界}=\max(T_\text{计算}, T_\text{通信}) \end{equation}\] \[\begin{equation} T_\text{上界} = T_\text{计算} + T_\text{通信} \end{equation}\]

实践中我们按下界优化，因为上下界最多差 2 倍。

计算受限 vs 通信受限

如果 $T_\text{计算} > T_\text{通信}$，说明计算是瓶颈，芯片算力被充分利用，这叫”计算受限“——这是好事！
如果 $T_\text{通信} > T_\text{计算}$，说明通信是瓶颈，芯片有一部分时间在”干等数据”，算力被浪费，这叫”通信受限“。

怎么快速判断会是哪种情况？用”算术强度“：

算术强度 = FLOPs 总量 / 需要搬运的字节数

\[\begin{equation} \text{算术强度} = \frac{\text{FLOPs}}{\text{字节数}} \end{equation}\]

直观理解：每搬运一字节数据，能做多少次运算。

同时，每个硬件有一个”临界算术强度“：

\[\text{临界强度} = \frac{\text{芯片 FLOPs/s}}{\text{带宽 Bytes/s}}\]

如果你的算法强度高于临界值 → 计算受限 ✅
如果你的算法强度低于临界值 → 通信受限 ❌

TPU v5e MXU 的临界强度大约是 240 FLOPs/字节（1.97×10¹⁴ / 8.2×10¹¹）。MXU 是 TPU 的矩阵乘法单元。TPU 还有 VPU 用于逐元素运算，临界强度不同。

举个例子：点积

计算两个 bfloat16 向量的点积 x · y（长度为 N）：

要加载：$x$ 和 $y$ 各 $2N$ 字节
要做：$N$ 次乘法 + $(N-1)$ 次加法 ≈ $2N$ 次运算
写回：$2$ 字节

\[\text{强度} = \frac{2N - 1}{4N + 2} \approx \frac{1}{2}\]

强度只有 0.5，远低于 240 的临界值——点积是典型的通信受限操作。点积实际在 VPU 上执行，不是 MXU。VPU 的临界强度约为 3，所以点积在 VPU 上也是通信受限的。

Roofline 图怎么看

Roofline 图是可视化这个权衡的好工具。X 轴是算术强度（对数），Y 轴是能达到的最大吞吐量（对数）。

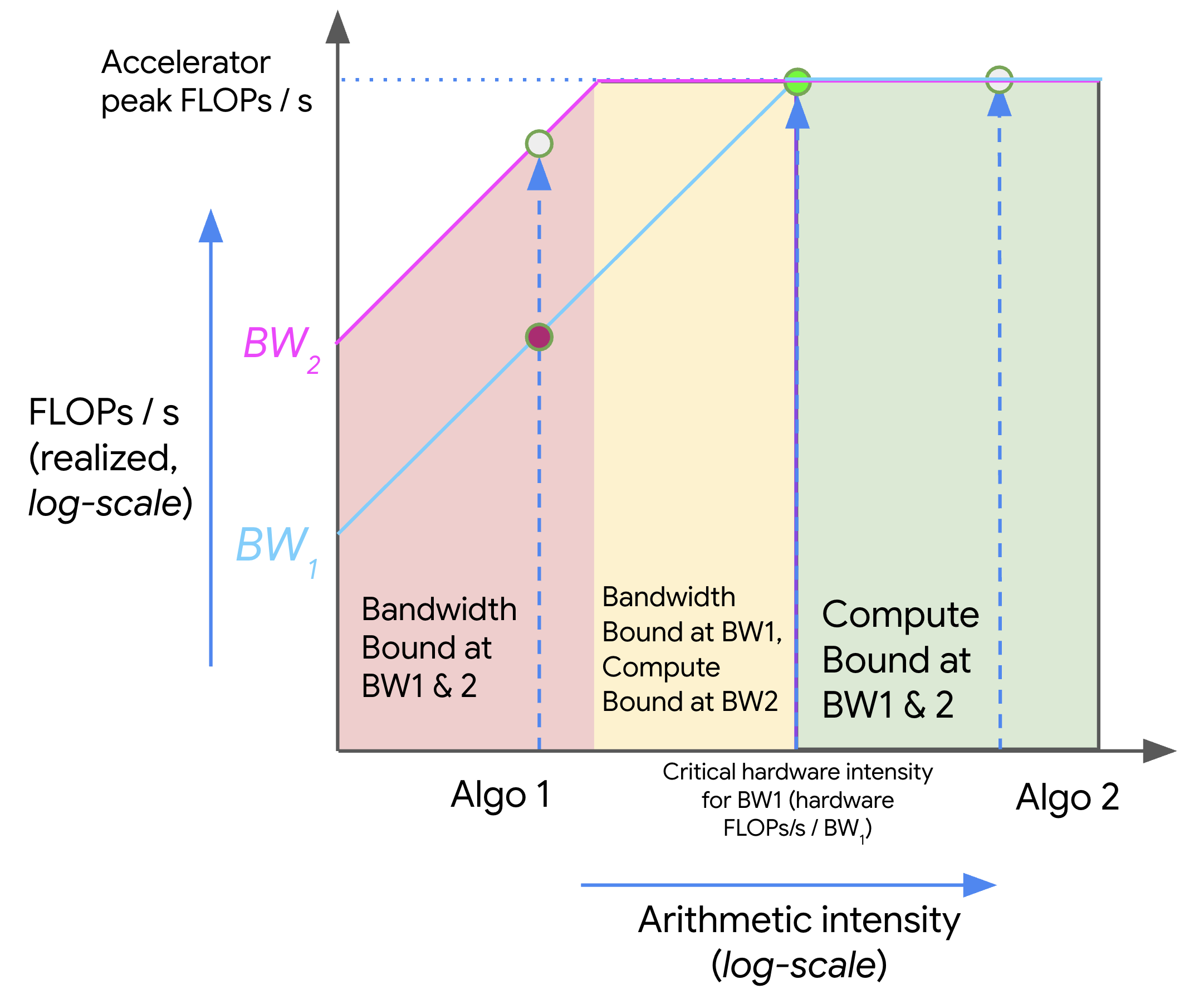
**Roofline 图解读：** 横轴是算术强度，纵轴是能达到的峰值吞吐量。红色区域：无论带宽多大都是通信受限。黄色区域：只在低带宽时受限。绿色区域：计算受限，充分利用了硬件算力。

图中可以看出：

强度低的算法（如 Algo 1）被”屋顶”的斜坡压住，无法达到峰值算力
强度高的算法（如 Algo 2）顶到了”天花板”，充分利用算力
提升性能的两个方向：提高算法强度 或 增加带宽

矩阵乘法的 Roofline

矩阵乘法（matmul）是深度学习的核心操作，来仔细算一下。

设 $X$ 的形状是 bf16[B, D]，$Y$ 是 bf16[D, F]，输出 $Z$ 是 bf16[B, F]：

加载：$2BD + 2DF$ 字节
计算：$2BDF$ FLOPs严格说是 $BDF$ 次乘法 + $BF(D-1)$ 次加法，约 $2BDF$。
写回：$2BF$ 字节

\[\text{强度} = \frac{2BDF}{2BD + 2DF + 2BF} = \frac{BDF}{BD + DF + BF}\]

如果 $B$ 相对于 $D$、$F$ 较小（这在 Transformer 中很常见），可以简化为：

\[\text{强度} \approx \frac{BDF}{DF} = B\]

所以当 $B > 240$ 时，矩阵乘法就变成计算受限！

黄金法则：bf16 矩阵乘法要在 TPU 上跑满算力，每副本 batch size 要大于 240 个 token。注意这是 token 数，不是序列数。比如 128 张 GPU 上跑 512 条 4096 token 的序列，总 batch = 512×4096 = 200 万 token，每卡 batch = 16k token，远超 240。

GPU 上这个数字稍高（约 300），但结论类似。

多卡通信的 Roofline

前面讲的都是单卡内部的 Roofline。但本书更关心的是多卡之间的通信。

举个例子：两张 TPU 联合做矩阵乘法，$X$ 和 $Y$ 沿 $D$ 维度各存一半。

做法是：

每张卡算自己那一半：TPU 0 算 X[:, :D/2] @ Y[:D/2, :]，TPU 1 算另一半
把结果（”部分和”）传给对方，加起来

计算时间减半了（两张卡分担）：

\[T_\text{计算} = \frac{BDF}{1.97 \times 10^{14}}\]

通信时间呢？要传的是 $2BF$ 字节的部分和：

\[T_\text{通信} = \frac{2BF}{4.5 \times 10^{10}}\]

临界条件变成了：

\[\frac{D}{2} > \frac{1.97 \times 10^{14}}{4.5 \times 10^{10}} = 4377\]

即 $D > 8755$ 时才是计算受限。

注意变化：单卡时临界值取决于 $B$（batch size），多卡时取决于 $D$（模型宽度）！想想为什么？

这类分析对于判断”能不能有效并行到多卡”至关重要。

练习题

题 1：int8 矩阵乘法

用 int8（每参数 1 字节）代替 bf16 做矩阵乘法 $X[B, D] \cdot Y[D, F] \rightarrow Z[B, F]$：

需要加载/写回多少字节？
需要多少 FLOPs？
算术强度是多少？
$T_\text{计算}$ 和 $T_\text{通信}$ 各是多少？整体运行时间的上下界？

假设 HBM 带宽 8.1×10¹¹ 字节/s，int8 峰值 3.94×10¹⁴ OPs/s。

点击查看答案

加载 $BD + DF$ 字节，写回 $BF$ 字节
还是 $2BDF$ FLOPs（只是精度变了）
强度 ≈ $2B$，临界值 = 3.94×10¹⁴ / 8.1×10¹¹ ≈ 486，所以 $B > 243$ 时计算受限。跟 bf16 差不多！
$T_\text{计算} = 2BDF / 3.94×10^{14}$，$T_\text{通信} = (BD + DF + BF) / 8.1×10^{11}$

题 2：int8 权重 + bf16 激活

实际中常见的做法是：权重量化成 int8，但激活和计算保持 bf16。即 bf16[B, D] × int8[D, F] → bf16[B, F]。

在什么 batch size 下会变成计算受限？（假设 1.97×10¹⁴ bf16 FLOPs/s）

点击查看答案

权重只要 $DF$ 字节（而不是 $2DF$），激活还是 $2BD$ 字节。

强度 ≈ $2BDF / DF = 2B$，临界条件 $2B > 240$，即 $B > 120$。

这比纯 bf16 的 240 低一半！说明权重量化能显著提高效率。

题 3：画个 Roofline 图

用题 2 的设置，分别对 $F = D = 4096$ 和 $F = D = 1024$ 画出 FLOPs/s vs $B$ 的曲线。

点击查看答案

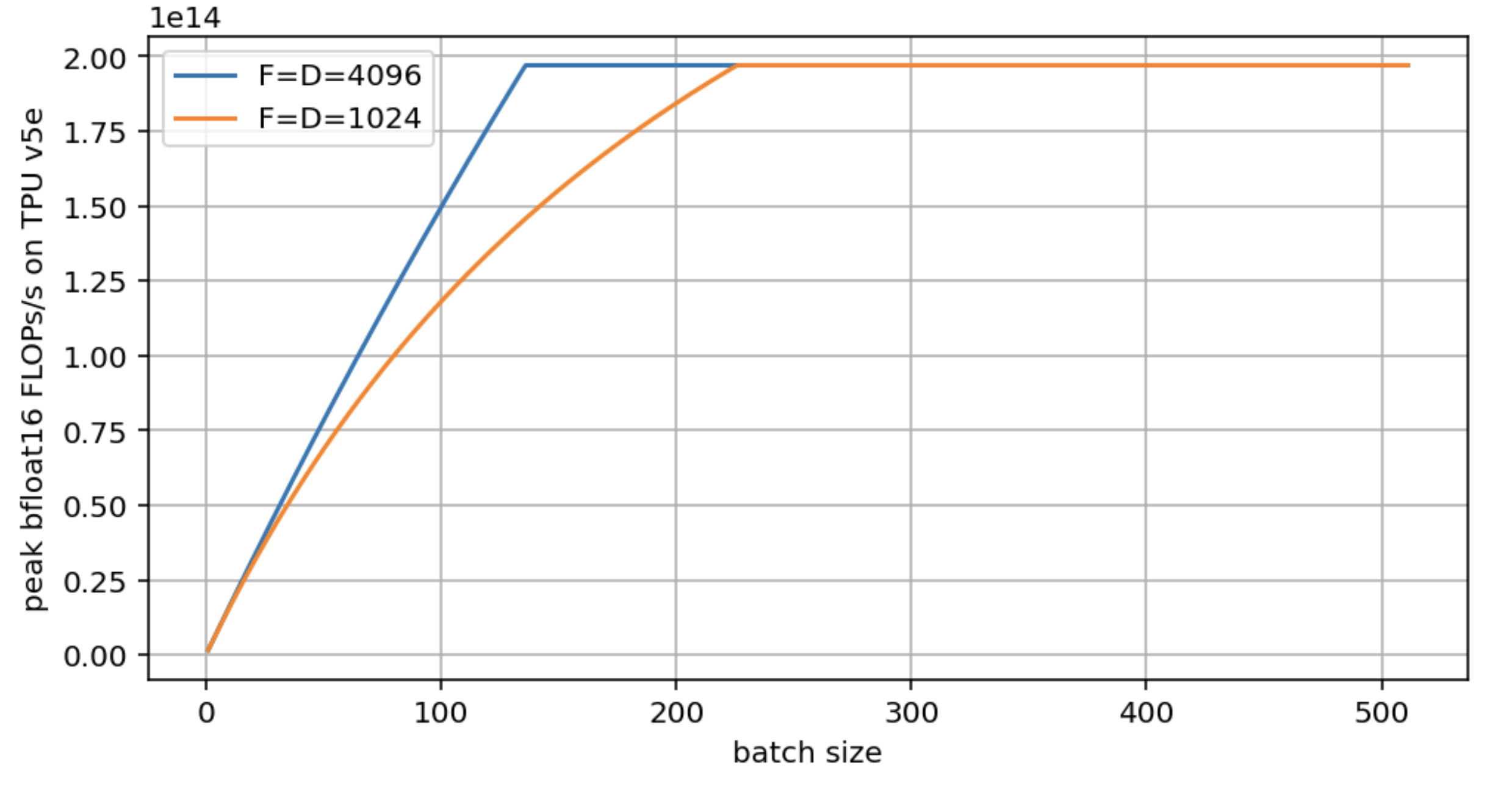
两个模型最终都能达到峰值算力，但大模型（D=4096）更早达到。小模型（D=1024）的临界 batch size 几乎翻倍。

import matplotlib.pyplot as plt
import numpy as np

bs = np.arange(1, 512)

def roofline(B, D, F):
  total_flops = 2*B*D*F
  flops_time = total_flops / 1.97e14
  comms_time = (2*B*D + D*F + 2*B*F) / 8.2e11
  total_time = np.maximum(flops_time, comms_time)
  return total_flops / total_time

plt.figure(figsize=(8, 4))
plt.plot(bs, roofline(bs, 4096, 4096), label='D=F=4096')
plt.plot(bs, roofline(bs, 1024, 1024), label='D=F=1024')
plt.legend()
plt.xlabel('Batch Size')
plt.ylabel('峰值 FLOPs/s (TPU v5e)')
plt.grid()

题 4：带 batch 维度的权重

如果权重矩阵每个 batch 不一样，即 int8[B, D] × int8[B, D, F] → int8[B, F]，算术强度是多少？

点击查看答案

FLOPs：还是 $2BDF$
通信：$BD + BDF + BF$（权重变成 $BDF$ 字节了！）
强度 ≈ $2BDF / BDF = 2$

强度变成常数了，跟 batch size 无关！这意味着几乎总是通信受限——很糟糕。

题 5：H100 的临界 batch size

查 H100 SXM 规格表，计算 bf16 矩阵乘法变成计算受限需要多大 batch。

注意：官方标称的 Tensor Core FLOPs 是有结构化稀疏加成的，实际要除以 2。

点击查看答案

标称 bf16 FLOPs：1.979×10¹⁵（带稀疏），实际约 10¹⁵
HBM 带宽：3.35TB/s

临界 batch = 10¹⁵ / 3.35×10¹² ≈ 298

和 TPU 差不多。

第 1 章完！下一章我们深入 TPU 的内部结构，点击继续。

Miscellaneous

^*Work done at Google DeepMind, now at MatX.

Citation

For attribution in academic contexts, please cite this work as:

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

or as a BibTeX entry:

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }