分片矩阵与矩阵乘法

Part 3 of How To Scale Your Model (第2部分：TPU | 第4部分：Transformer 数学)

模型太大放不下一张卡？那就切成块分到多张卡上！这叫『分片』。问题是：切完之后怎么算矩阵乘法？这一章用简单的符号系统，把分片矩阵乘法的各种情况讲清楚。

什么是分片？

在上万张 TPU/GPU 上训练大模型，我们做的计算和单卡是一样的——区别在于数组太大，一张卡放不下，所以必须切成块分到多张卡上。有时候即使放得下，我们也会分片——多卡并行可以加速。比如推理时为了降低延迟，训练时为了缩短每步时间。

这种”切块分配”就叫分片（Sharding）或分区（Partitioning）。扩展的核心问题是：怎么分片才能保持高效？

看个例子——一个 2D 数组分到 4 张 TPU 上：

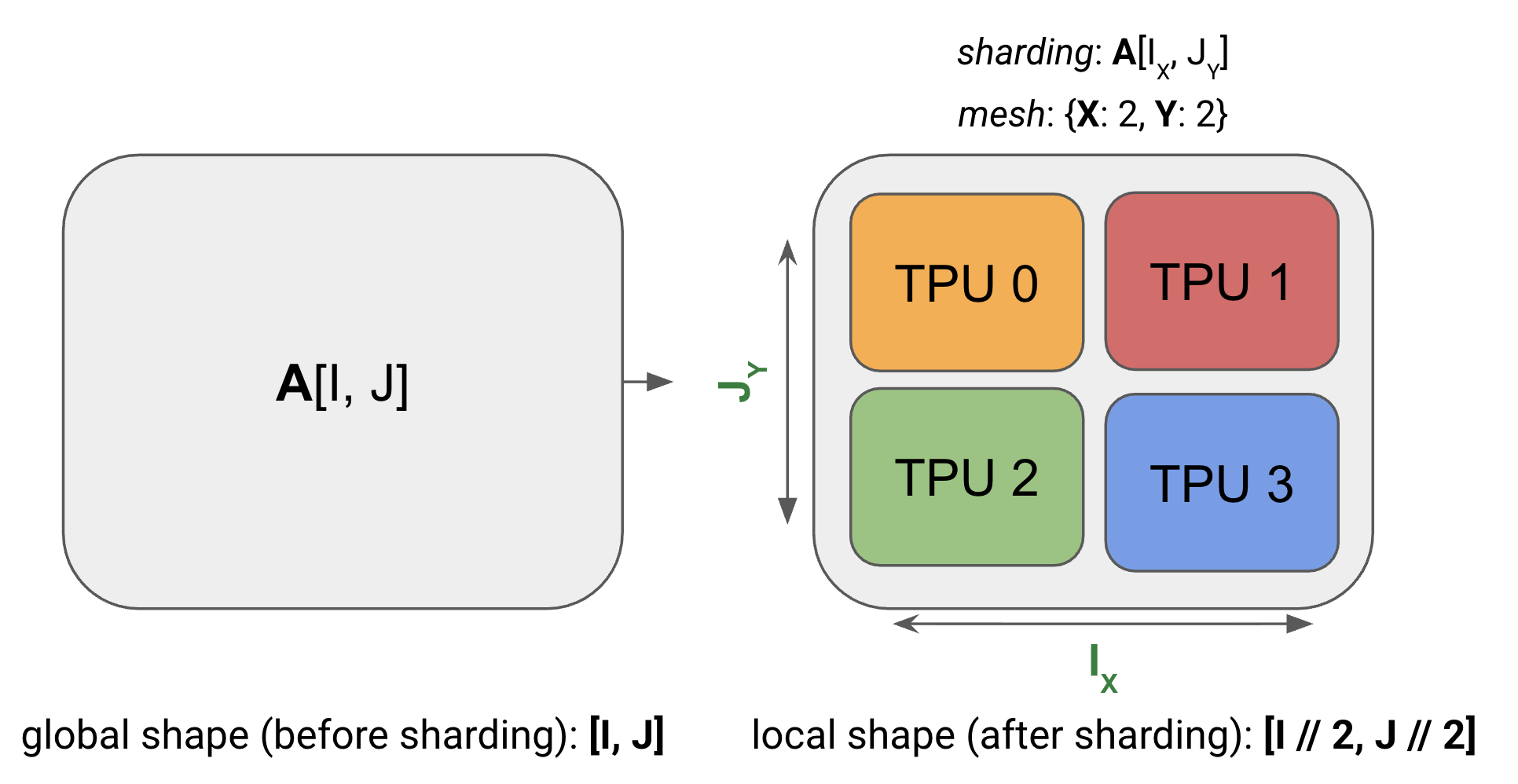
**分片示意：** 一个 A[I, J] 数组分到 4 张卡上，两个维度各切一半，变成 A[I_X, J_Y]。每张卡只存 1/4 的数据。

注意：分片后的数组还是有”全局形状”的（比如 [4, 128]），但每张卡实际只存一部分（比如 [2, 64]）。

分片符号系统

我们用一套命名轴符号来描述分片。先定义两个概念：

设备网格（Device Mesh）：把物理设备排成 2D 或 3D 网格，每个轴取个名字，如 X、Y、Z
分片（Sharding）：数组的每个维度分到网格的哪个轴上

例子（上图）：

网格：Mesh(devices=((0,1),(2,3)), axis_names=('X','Y'))——4 张 TPU 排成 2×2，轴名叫 X 和 Y
分片：A[I_X, J_Y]——第一维 I 沿 X 切，第二维 J 沿 Y 切

结合起来：每张卡存的是 (|I|/2, |J|/2) 大小的块。

小测验： 数组 fp32[1024, 4096] 分片为 A[I_XY, J]，网格 {'X':8, 'Y':2}。每张卡存多少数据？在 H100 上加载要多久（带宽 3.4TB/s）？

答案

I_XY 表示第一维沿 X 和 Y 一起切（16 份），第二维不切。

每卡形状：fp32[64, 4096] = 1MB

加载时间：1e6 / 3.4e12 ≈ 0.3μs（实际可能更长，因为数据太小，开销占主导）

更多分片方式图解：

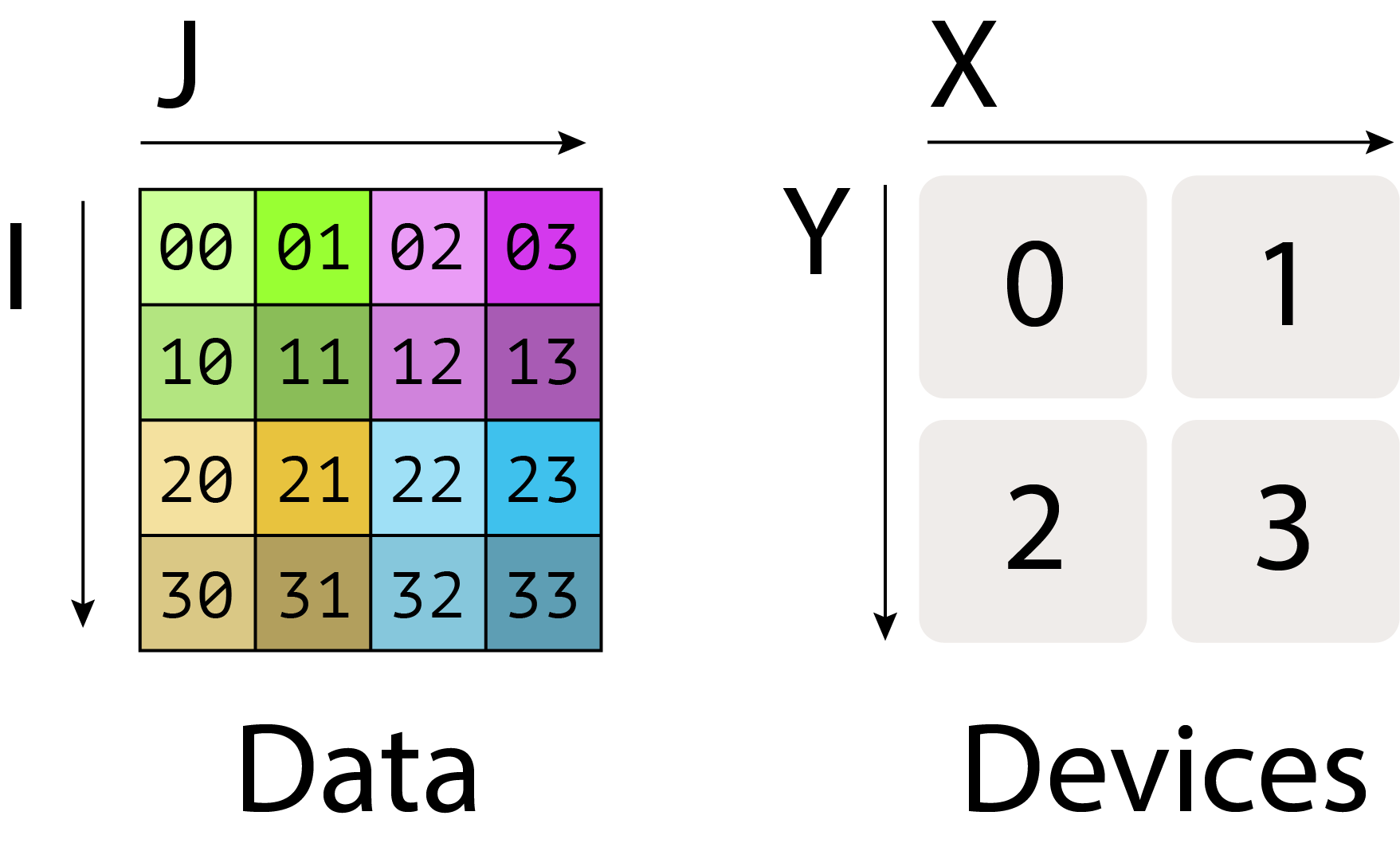
A[I, J]（没下标）= 完全复制：每张卡都有完整副本。

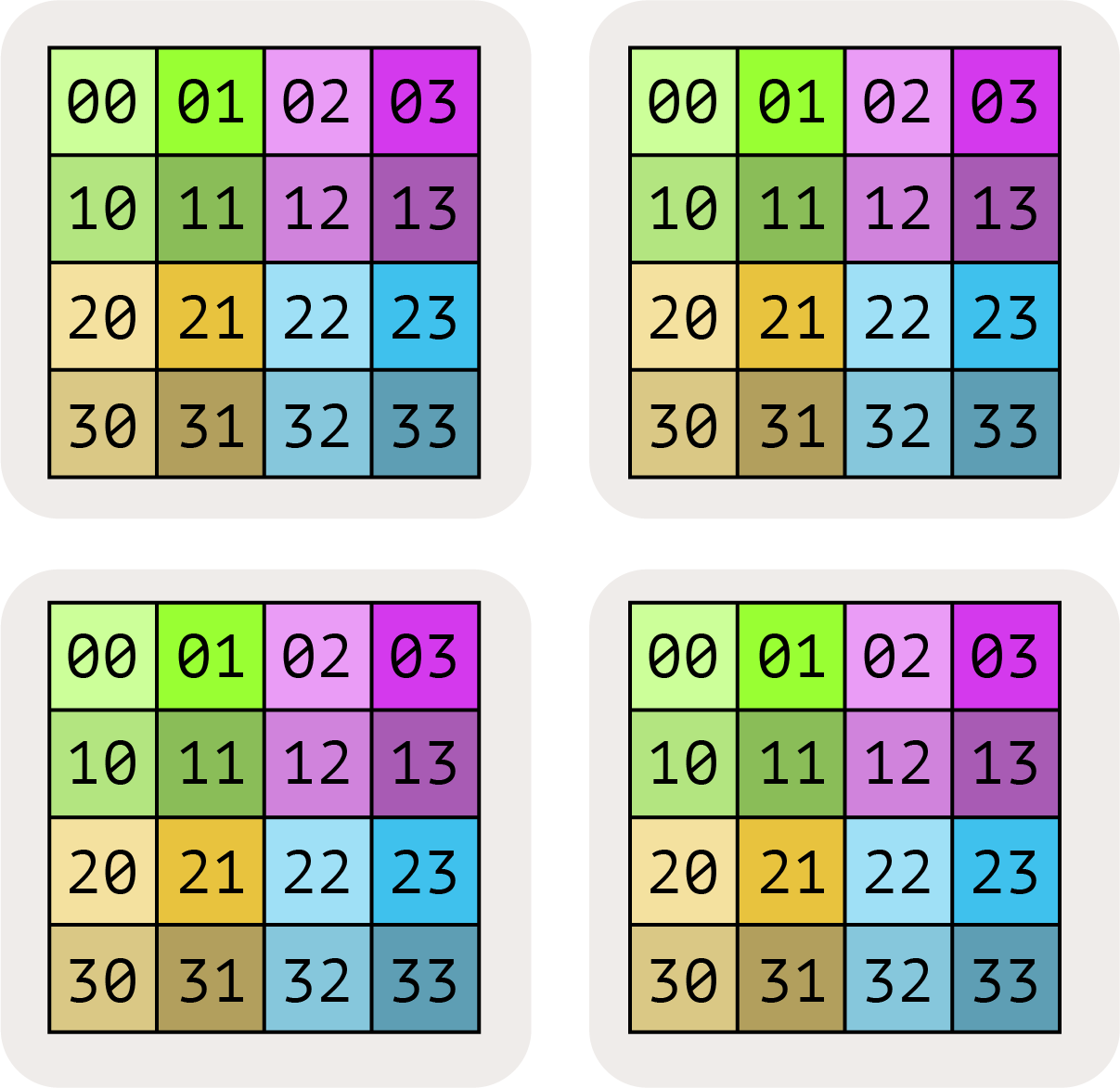
A[I_X, J] = I 轴沿 X 切，J 轴不切（沿 Y 部分复制）。

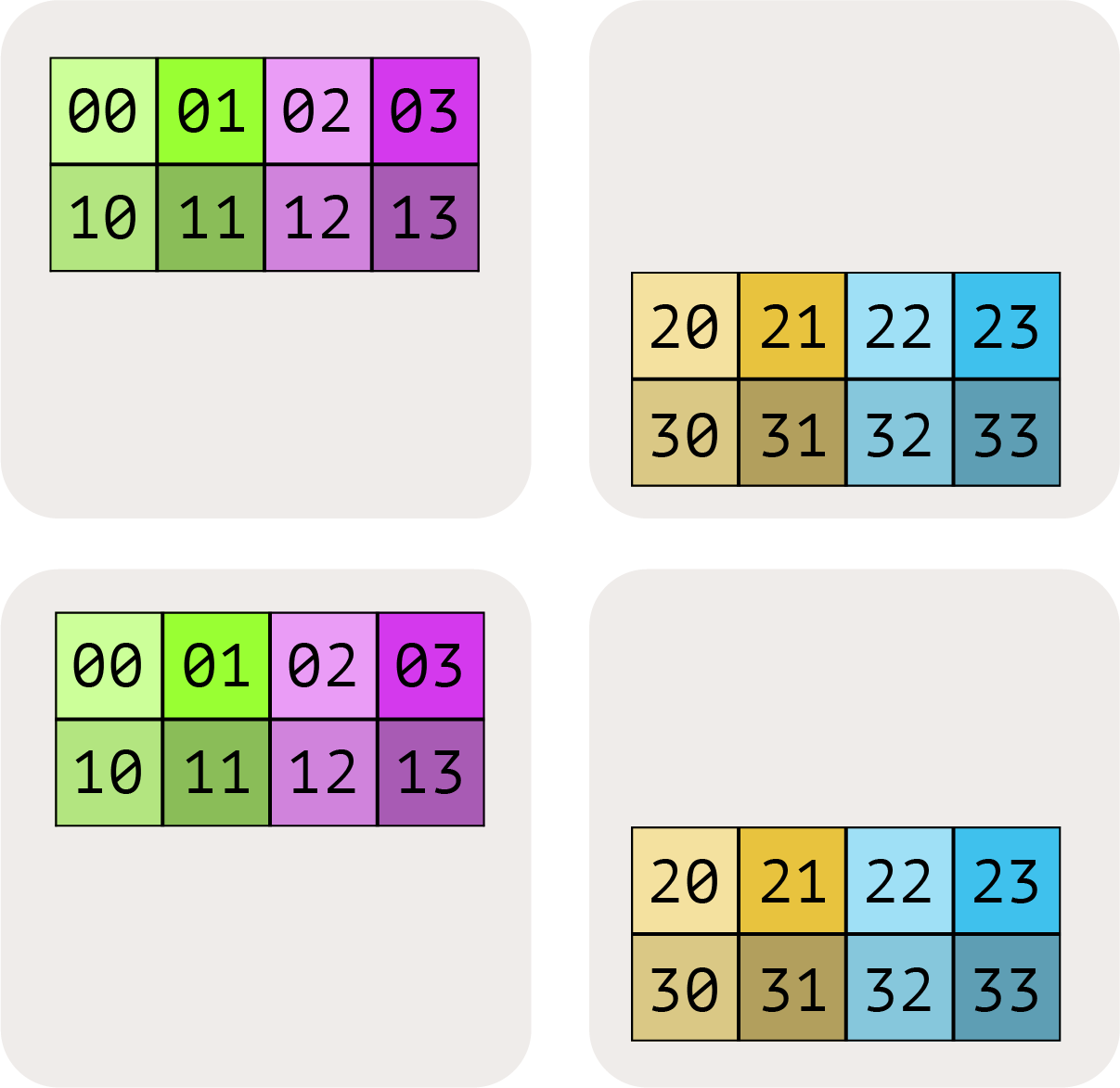
A[I_X, J_Y] = 两个维度分别沿 X 和 Y 切。

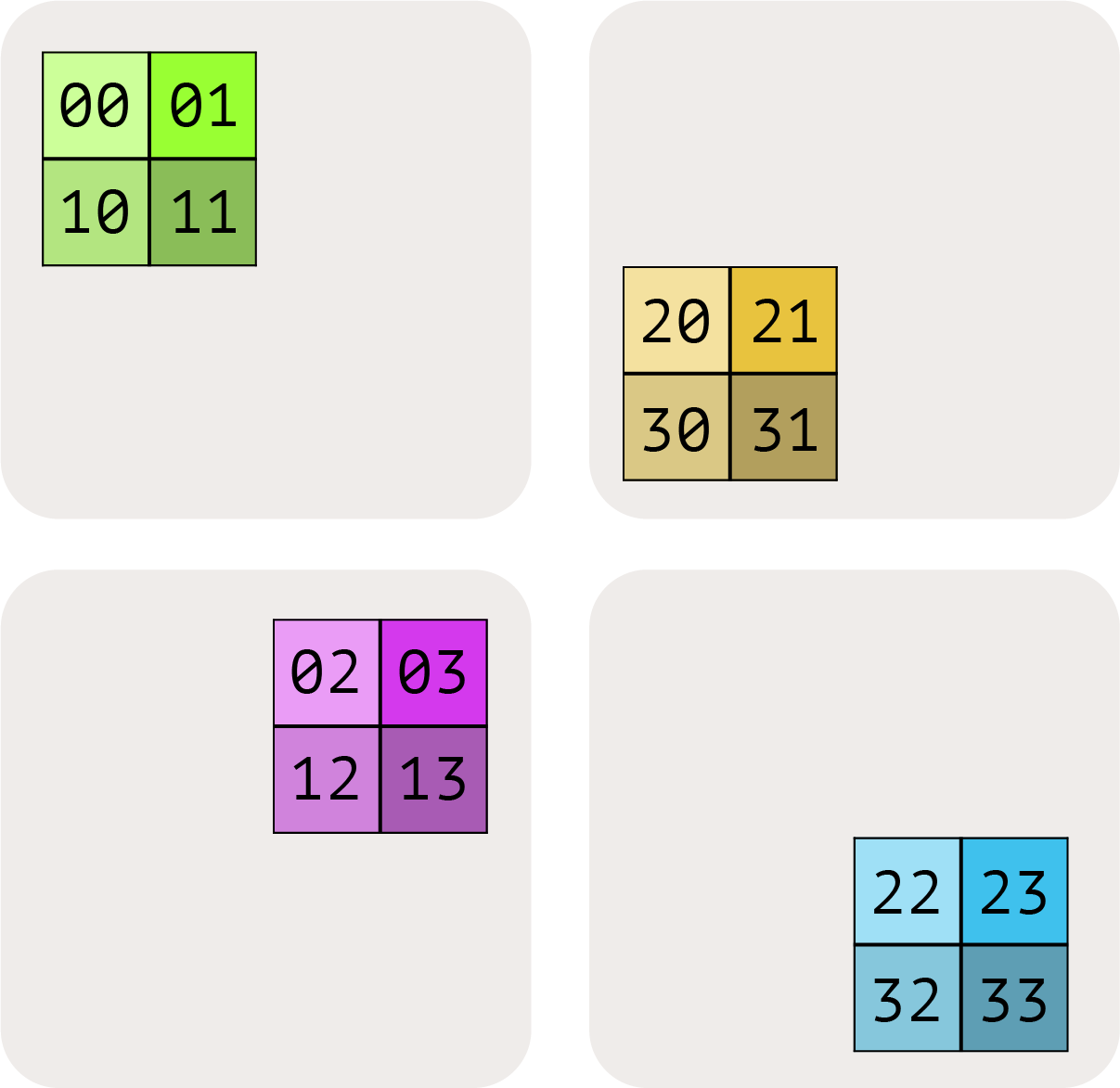
A[I_XY, J] = 把 X 和 Y 当作一个大轴，I 沿这个大轴切。下标顺序很重要，决定了遍历顺序。

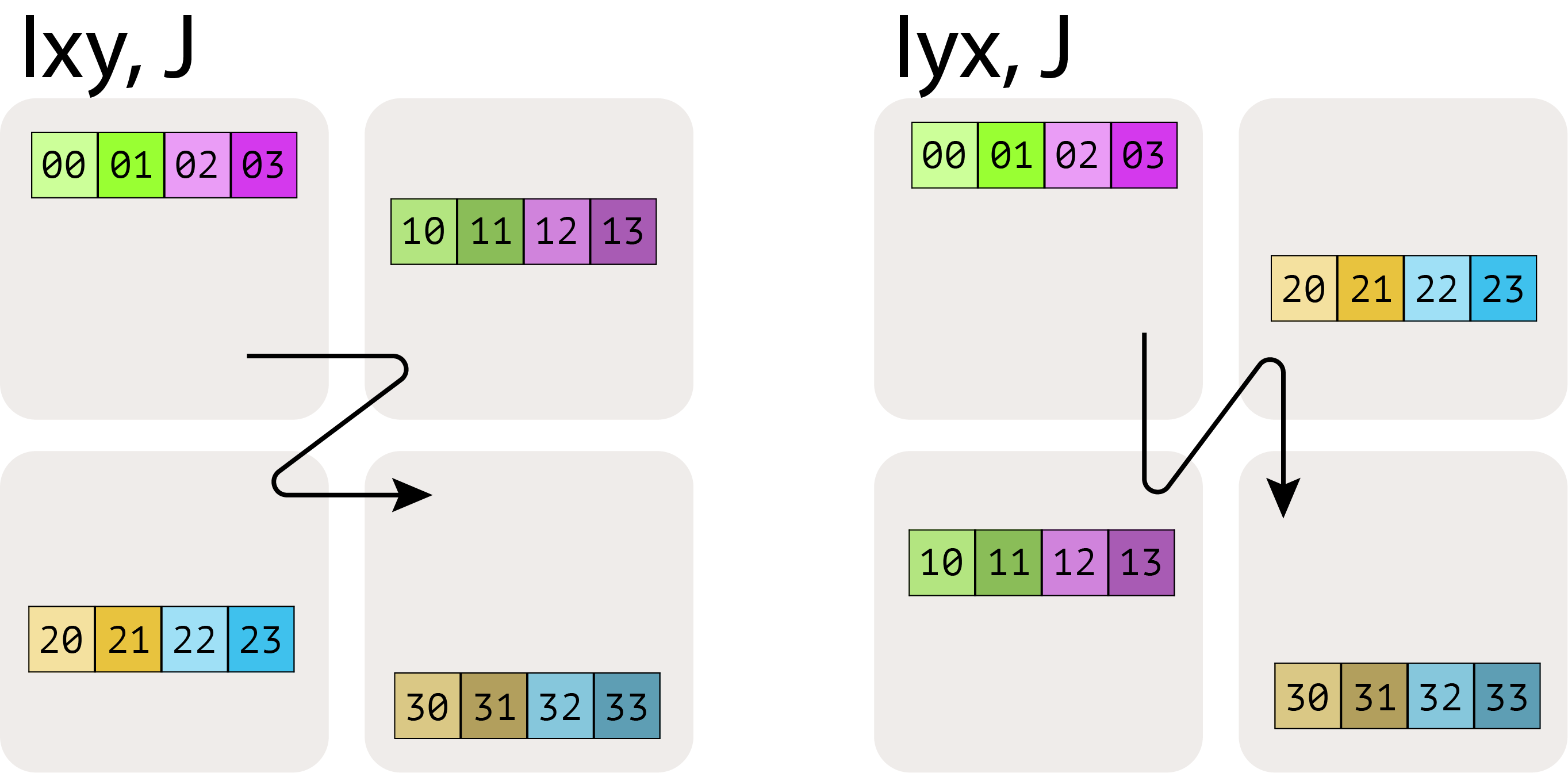
禁止：A[I_X, J_X]——同一个网格轴不能用两次！一个轴”用完”就没了。

小测验： A: int8[128, 2048] 分片为 A[I_XY, J]，网格 {'X':2, 'Y':8, 'Z':2}。每卡多大？总共占多少内存？

答案

I 沿 XY 切（16 份），J 不切，Z 轴复制
每卡：int8[8, 2048] = 16KB
Z=2 份副本 × 原数组 128×2048 = 512KB 总计
验证：32 卡 × 16KB = 512KB ✓

JAX 代码示例

来看看实际代码怎么写（可以在 Colab 上玩）：

import jax
import jax.numpy as jnp

# 1. 创建网格：8 张 TPU 排成 4×2，轴名 X 和 Y
mesh = jax.make_mesh((4, 2), ('X', 'Y'))

# 2. 定义分片的辅助函数
def P(*args):
  return jax.NamedSharding(mesh, jax.sharding.PartitionSpec(*args))

# 3. 创建分片数组
A = jnp.zeros((8, 2048), dtype=jnp.bfloat16, device=P('X', 'Y'))  # A[I_X, J_Y]
B = jnp.zeros((2048, 8192), dtype=jnp.bfloat16, device=P(None, 'Y'))  # B[J, K_Y]

# 4. 执行矩阵乘法——JAX 自动处理分片通信！
y = jax.jit(lambda A, B: jnp.einsum('BD,DF->BF', A, B), 
            out_shardings=P('X', 'Y'))(A, B)

JAX 的魔法：分片数组用起来和普通数组一样！B.shape 显示的是全局形状 (2048, 8192)，但实际上每张卡只存一部分。JAX/XLA 会自动插入必要的通信。

分片矩阵怎么乘

分布式数据怎么做计算？

逐元素操作：没开销，各算各的
矩阵乘法：有点复杂，但好在 LLM 主要就是矩阵乘法

关键观察：不同分片方式需要不同的通信。

比如 A[I_X, J] · B[J, K_Y] → C[I_X, K_Y] 可以直接本地算，不用通信——因为收缩维度 J 没分片。

但如果想要输出不分片 C[I, K]，就得先把 A 或 B 收集到每张卡上（用 AllGather），或者把结果收集起来。

用”分块矩阵乘法”来理解

矩阵可以看成”块的矩阵”：

\[\begin{pmatrix} A_{00} & A_{01} \\ A_{10} & A_{11} \end{pmatrix} \cdot \begin{pmatrix} B_{00} & B_{01} \\ B_{10} & B_{11} \end{pmatrix} = \begin{pmatrix} A_{00}B_{00}+A_{01}B_{10} & A_{00}B_{01}+A_{01}B_{11} \\ A_{10}B_{00}+A_{11}B_{10} & A_{10}B_{01}+A_{11}B_{11} \end{pmatrix}\]

分布式矩阵乘法就是：搬块 → 本地乘 → 求和。问题是搬运的开销是多少。

四种基本情况：

情况	描述	解决方案
1	收缩维度都没分片	直接本地乘，不用通信
2	一边收缩维度分片了	先 AllGather 那一边
3	两边收缩维度都分片了	本地乘，再 AllReduce 结果
4	非收缩维度撞车了	先 AllGather 其中一边

情况1：收缩维度没分片

最理想的情况——两边都没有在收缩维度上分片：

\[A[I_X, J] \cdot B[J, K_Y] \to C[I_X, K_Y]\]

每张卡可以独立计算，结果自然就是正确的分片形式。以下都行：

\[\begin{align*} A[I, J] \cdot B[J, K] &\to C[I, K] \\ A[I_X, J] \cdot B[J, K] &\to C[I_X, K] \\ A[I, J] \cdot B[J, K_Y] &\to C[I, K_Y] \\ A[I_X, J] \cdot B[J, K_Y] &\to C[I_X, K_Y] \end{align*}\]

情况2：一边的收缩维度分片了

比如：

\[A[I, J_X] \cdot B[J, K] \to C[I, K]\]

问题：A 的 J 维度被切开了，但 B 是完整的。不能直接乘。

解决方案：先把 A 收集完整（AllGather），再乘：

$\text{AllGather}_X(A[I, J_X]) \to A[I, J]$ $A[I, J] \cdot B[J, K] \to C[I, K]$

**要点**：收缩维度分片了？先 AllGather 收集完整，再算。

什么是 AllGather？

AllGather 把分散在各卡的分片收集到每张卡上，变成完整副本：

\[\text{AllGather}_{XY}(A[I_{XY}, J]) \to A[I, J]\]

**AllGather 动画：** 8 张卡，每张从 1/8 数据开始，传递一圈后每张都有完整副本。

AllGather 要多久？

设数组大小 $V$ 字节，沿大小为 $X$ 的轴收集，双向 ICI 带宽 $W$：

\[T = \frac{V}{W}\]

惊人发现：时间和 X 无关！ 不管分成多少份，只要带宽能跑满，总时间只取决于数据量。

**要点**：AllGather/ReduceScatter/AllReduce 的时间只取决于数据量和带宽，和分片数量无关（带宽受限时）。

延迟受限的情况：每跳有约 1μs 的固有延迟。如果分片太小（<45KB），就变成延迟受限，时间会依赖跳数。

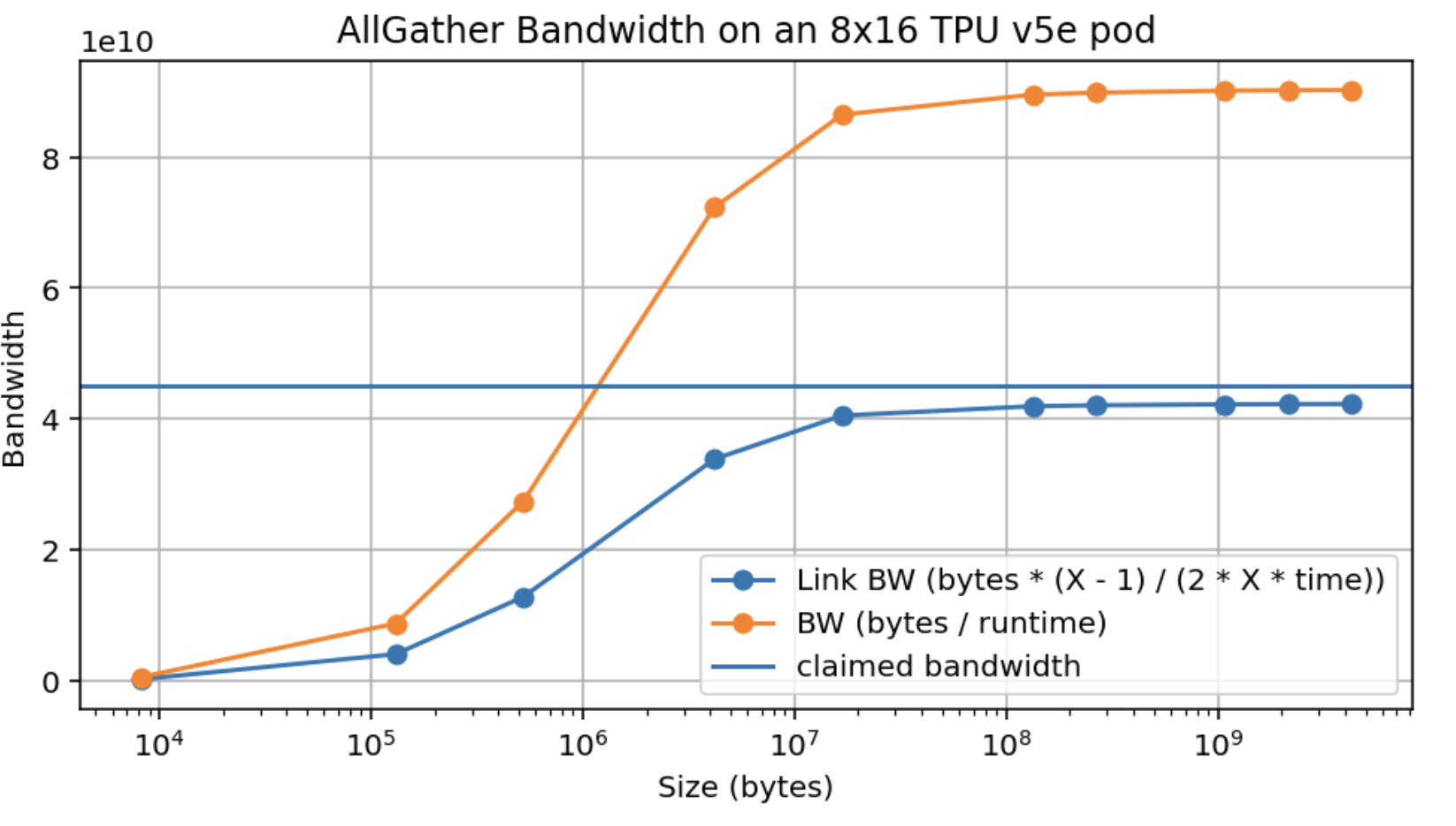
**实测 AllGather 带宽**：约 10MB 时达到峰值，接近理论值的 95%。

多轴 AllGather：沿多个轴收集时，可用带宽成倍增加。

小测验： TPU v5e 8×16，网格 {'X':8, 'Y':4}。AllGather_Y(A[E_Y, F]) → A[E, F]，E=2048，F=8192（bf16）要多久？E=256，F=256 呢？

答案

v5e 双向 ICI 带宽 9×10¹⁰ B/s
大数组：34MB / 9×10¹⁰ ≈ 377μs
- 注意：4×4 的 Y 轴没有环绕链路，实际约 560-680μs
小数组：256×256×2 = 128KB，每分片 32KB
- 32KB / 4.5×10¹⁰ ≈ 0.7μs，是延迟受限的
- 3 跳 × 1μs ≈ 3μs（实测约 8μs）

情况3：两边的收缩维度都分片了

\[A[I, J_X] \cdot B[J_X, K] \to C[I, K]\]

两边的 J 都沿 X 切了。好消息是可以先本地乘，但每张卡只算了部分和：

\[A[I, J_X] \cdot_\text{本地} B[J_X, K] \to C[I, K]\{U_X\}\]

{U_X} 表示”沿 X 还没归约”——结果不完整，需要把所有卡的部分和加起来。

解决方案：AllReduce

\[\text{AllReduce}_X(C[I, K]\{U_X\}) \to C[I, K]\]

AllReduce = ReduceScatter + AllGather，成本是 AllGather 的 2 倍。

**ReduceScatter 动画**：边传边加，最后每张卡得到结果的一个分片。

成本公式：

$T_\text{AllGather 或 ReduceScatter} = \frac{V}{W}$ $T_\text{AllReduce} = 2 \times \frac{V}{W}$

情况4：非收缩维度撞车了

$A[I_X, J] \cdot B[J, K_X] \to C[I_X, K_X]$ ❌

问题：X 轴被用了两次！第 i 张卡只有 C 的 (i,i) 块——对角线，其他部分没法算。

解决方案：先 AllGather 其中一边：

方案 A： $\text{AllGather}_X(A[I_X, J]) \to A[I, J]$ $A[I, J] \cdot B[J, K_X] \to C[I, K_X]$

方案 B： $\text{AllGather}_X(B[J, K_X]) \to B[J, K]$ $A[I_X, J] \cdot B[J, K] \to C[I_X, K]$

选哪个取决于后续计算需要什么分片。

四大通信原语详解

总结一下前面用到的通信操作：

原语	作用	符号变化	成本
AllGather	收集分片	`[A_X, B] → [A, B]`	V/W
ReduceScatter	归约+分片	`[A, B]{U_X} → [A_X, B]`	V/W
AllReduce	归约到每张卡	`{U_X} → 无`	2V/W
AllToAll	换一种分片方式	`[A_X, B] → [A, B_X]`	V/(4W)

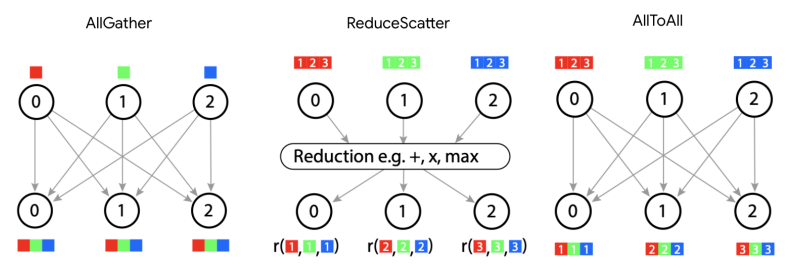
AllToAll：最后一个原语

AllToAll 是”重新分片”——把下标从一个维度移到另一个：

\[\text{AllToAll}_{X,J}(A[I_X, J]) \to A[I, J_X]\]

它比 AllGather 便宜，因为不需要把每个分片复制到所有卡：

\[T_\text{AllToAll} = \frac{V}{4W}\]

**AllToAll 动画**：每张卡只把数据发到需要的目标卡，不是广播给所有卡。

ReduceScatter 补充

ReduceScatter 是 AllGather 的”导数”——反向传播时互为转置：

前向 AllGather [A_X] → [A] → 反向 ReduceScatter [A']{U_X} → [A'_X]
前向 ReduceScatter → 反向 AllGather

数学细节

广播和归约是转置关系： $\text{broadcast}: \mathbb{R}^n \to \mathbb{R}^{pn}, \quad \text{broadcast} = u \otimes I_n$ $\text{reduce}: \mathbb{R}^{pn} \to \mathbb{R}^n, \quad \text{reduce} = u^T \otimes I_n$

AllGather 和 ReduceScatter 是它们的扩展，同样互为转置。

实用技巧：AllReduce = ReduceScatter + AllGather。有时候我们可以只做 ReduceScatter，把结果保持分片状态：

$A[I, J_X] \cdot B[J_X, K] \to C[I, K]\{U_X\}$ $\text{ReduceScatter}_{X,K}(C)\{U_X\} \to C[I, K_X]$

这样更便宜，但输出变成分片的了。

本章小结

分片 = 网格 + 分片规则
- 网格：设备怎么排列，轴叫什么名
- 分片：数组的哪个维度沿哪个轴切
分片计算和普通计算一样，除非收缩维度被分片了
- 情况1：收缩维度没分片 → 直接算
- 情况2：一边分片了 → AllGather 那一边
- 情况3：两边都分片了 → 本地算 + AllReduce/ReduceScatter
- 情况4：非收缩维度撞车 → AllGather 其中一边
四大原语：
- AllGather：收集分片
- ReduceScatter：归约+重新分片
- AllReduce：归约到每张卡（= RS + AG）
- AllToAll：换一种分片方式
成本和分片数无关，只和数据量有关（带宽受限时）

操作	成本
AllGather / ReduceScatter	V / W
AllReduce	2 × V / W
AllToAll	V / (4W)

练习题

题 1：数组 A[I_X, J, K, ...] 分到 {'X':4, 'Y':8, 'Z':2} 网格上，总内存是单副本的多少倍？

答案

沿 X 切 4 份，沿 Y 和 Z 复制。总共 8×2 = 16 份。

题 2：TPU v4p 4×4×4 切片，网格 {'X':4, 'Y':4, 'Z':4}（有环绕链路，双向 9×10¹⁰ B/s）。

AllGather_X(A[B_X, D_Y])，B=1024，D=4096（bf16）要多久？
AllGather_XY(A[B_X, D_Y]) 呢？
AllReduce_Z(A[B_X, D_Y]{U_Z}) 呢？

答案

实际收集的是 2BD/Y = 2×1024×4096/4 字节在 1 个轴上。$T = 2BD/(Y×W) = 23μs$
两倍带宽，完整数组：$T = 2BD/(2W) = 46μs$
AllReduce 是 AllGather 的 2 倍，分片大小 2BD/(XY)：$T = 4BD/(16W) ≈ 12μs$

题 3：TPU v4p 4×4×4，收集 bf16[128] 要多久？

答案

只有 256 字节，每卡 64 字节。延迟受限！2 跳 × 1μs ≈ 2μs。

题 4：执行 X[B, D] ·_D Y[D_X, F] → Z[B, F]，有两种策略：

策略1：先 AllGather Y，再乘
策略2：先本地乘得部分和，再 AllReduce

各自的 FLOPs 和通信成本是多少？哪个更好？

答案

策略1：

AllGather：2DF/W
FLOPs：2BDF/C（每卡都做完整乘法）
总时间：max(2BDF/C, 2DF/W)

策略2：

FLOPs：2BDF/(XC)（计算量分摊）
AllReduce：4BF/W
总时间：max(2BDF/(XC), 4BF/W)

策略2 通常计算受限（D 通常很大），变成 4BF/W。策略1 在小 batch 时通信受限，是 2DF/W。

比较：4BF/W vs 2DF/W → 当 D > 2B 时策略2 更好。对大模型（D 大）通常如此。

实际上：这种情况不常见，因为 FSDP 下激活也是分片的。

题 5：TPU v5p 4×4×4 上算 A[I, J] · B[J, K] → C[I, K]，最低延迟。输入可以任意分片，输出要完全复制。怎么分片？

部分答案

几种选项：

A[I_XYZ, J] · B[J, K] + 最后 AllGather
A[I, J] · B[J, K_XYZ] + 最后 AllGather
A[I, J_XYZ] · B[J_XYZ, K] + 最后 AllReduce
完全复制（重复计算）

(1) 和 (2) 成本相同。比较通信成本即可。

题 6：TPU v5e 4×4 上算：

A[I_X, J_Y] · B[J_Y, K] → C[I_X, K]
A[I_X, J] · B[J_X, K_Y] → C[I_X, K_Y]（标准 FSDP + TP）
A[I_X, J] · B[J, K_Y] → C[I_X, K_Y]（纯 TP + DP）

分别要什么通信？时间是多少？

题 7：Transformer 块有 W_in[D, F] 和 W_out[F, D]，F » D。取 D=8192，F=32768，B=128（bf16）。在 TPU v5e 2×2 上，每卡只有 300MB 空闲内存。怎么分片？

部分答案

权重每个 536MB，必须分片。两种思路：

FSDP：In[B_X, D] · W_in[D_XY, F] · W_out[F, D_XY]（需要先 AllGather 权重）
TP：In[B, D_XY] · W_in[D, F_XY] · W_out[F_XY, D]（开始 AllGather，结束 ReduceScatter）

TP 通常更好，因为激活小，通信成本低。

题 8 [挑战]：用 JAX 实现并测量四大原语的性能：jax.lax.all_gather、jax.lax.psum、jax.lax.psum_scatter、jax.lax.all_to_all。

题 9：情况2 还有另一种策略——不 AllGather，而是本地乘再 AllReduce：

$A[I, J_X] \cdot_\text{本地} B[J_X, K] \to C[I, K]\{U_X\}$ $\text{AllReduce}_X(C) \to C[I, K]$

写出具体算法
如果接受输出分片呢？
和原策略的通信成本比较？

答案

每卡用自己那部分 J 做外积，得到部分和，再 AllReduce
可以用 ReduceScatter 代替 AllReduce，更便宜
AllGather A：通信量 ∝ NM。ReduceScatter C：通信量 ∝ NK。比值 = M/K。

题 10 [挑战]：为什么双向环的 AllToAll 是 AllGather 的 1/4？

答案

单向环：

AllGather：每个分片传 D-1 次 → 总量 ∝ N² × (D-1)/D ≈ N²
AllToAll：第 i 块只传 i 跳 → 总量 ∝ N² × D(D-1)/2 / D² ≈ N²/2

双向环：

AllGather 快 2 倍 → N²/2
AllToAll 快 4 倍（最远只需 D/2 跳）→ N²/8

比值：(N²/2) / (N²/8) = 4

第 3 章完！下一章学习 Transformer 数学，点击继续。

Miscellaneous

^*Work done at Google DeepMind, now at MatX.

Citation

For attribution in academic contexts, please cite this work as:

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

or as a BibTeX entry:

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }