Transformer 数学完全指南

Part 4 of How To Scale Your Model (第3部分：分片 | 第5部分：训练)

Transformer 到底有多少参数？训练一次要算多少次乘法？KV 缓存有多大？这一章把这些数学算清楚。

从矩阵乘法说起

先回顾一下基本的矩阵乘法计算量：

\[\begin{array}{cc} \textrm{数组} & \textrm{形状} \\ \hline x & \textrm{[P]} \\ y & \textrm{[P]} \\ A & \textrm{[N, P]} \\ B & \textrm{[P, M]} \\ \end{array}\]

向量点积 $x \cdot y$：P 次乘法 + P 次加法 = 2P FLOPs
矩阵-向量乘 $Ax$：N 次点积 = 2NP FLOPs
矩阵-矩阵乘 $AB$：M 列，每列一次矩阵-向量乘 = 2NPM FLOPs

一般规则：两个张量相乘时，收缩维度和批次维度只算一次，其他维度全乘起来，最后乘 2。

\[\begin{array}{ccc} \textrm{操作} & \textrm{FLOPs} & \textrm{数据量} \\ \hline x \cdot y & 2P & 2P \\ Ax & 2NP & NP + P \\ AB & 2NPM & NP + PM \\ \end{array}\]

关键观察：矩阵乘法的计算量是 $O(N^3)$，数据量只有 $O(N^2)$——矩阵越大，越容易跑满算力！这就是为什么 Transformer 这种”矩阵乘法为主”的架构这么适合扩展。

训练比推理贵 3 倍

推理只需要前向传播：A · B → C，花 2NPM FLOPs。

训练还要反向传播，算两个梯度：

\[\frac{\partial L}{\partial B} = A^T \cdot \frac{\partial L}{\partial C} \quad (2NPM)\] \[\frac{\partial L}{\partial A} = \frac{\partial L}{\partial C} \cdot B^T \quad (2NPM)\]

加起来：前向 2NPM + 反向 4NPM = 6NPM FLOPs

这就是著名的 6 × 参数量 × token 数 公式的来源：训练时，每个 token 大约要 6 倍于参数量的运算。

Transformer 各部分的计算量

Transformer 是当今的主流架构。这里不重新介绍它是什么（可以参考这篇图解），但我们会仔细算一下每个组件的计算量。

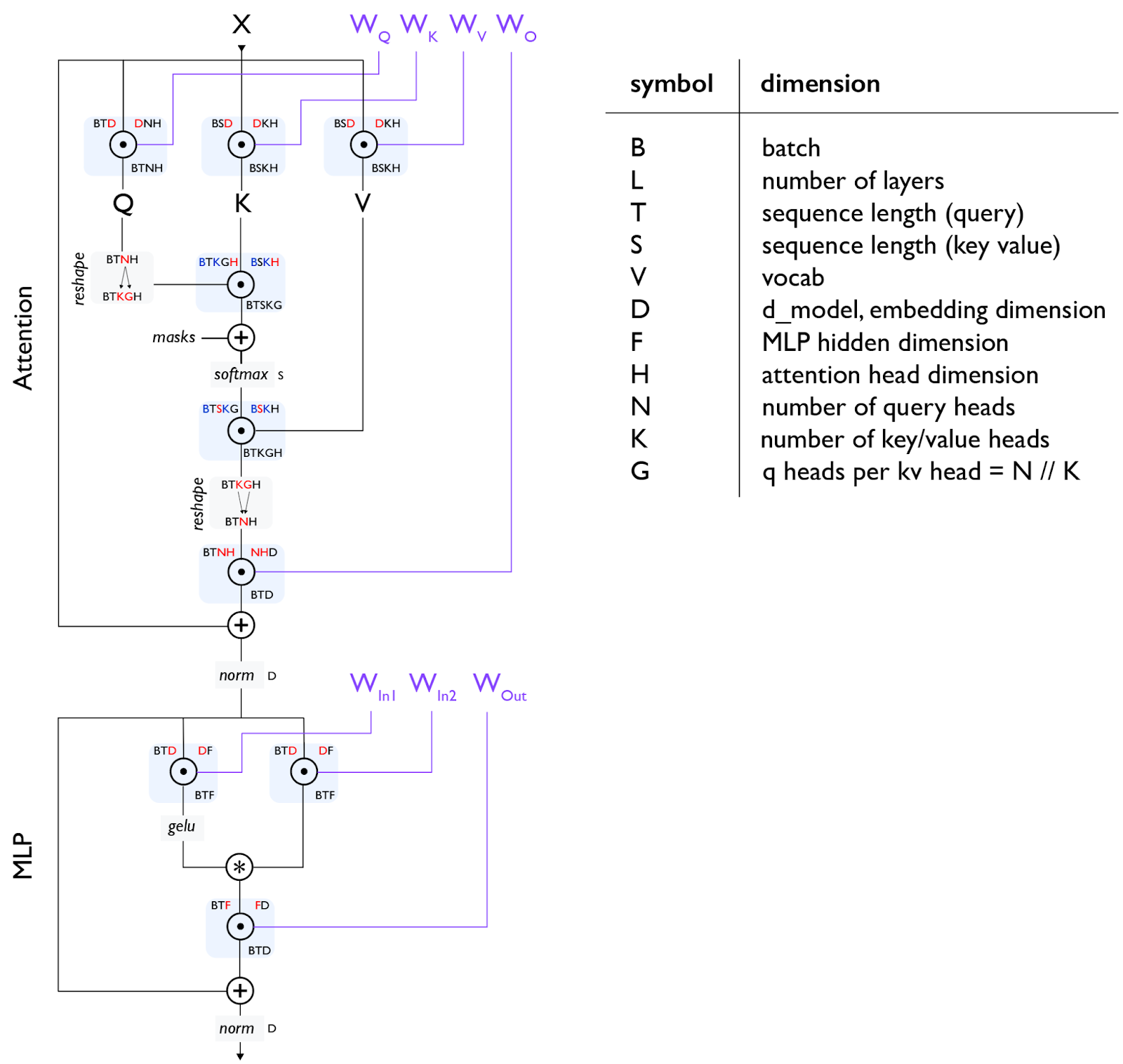
**Transformer 一层的结构图**：从上到下流动。红色是收缩维度，蓝色是批次维度。每个矩阵乘法显示输入形状（左上）、权重形状（右上）、输出形状（下方）。

符号说明：

B = 批次大小
T = 序列长度（Query）
S = 序列长度（Key/Value），自注意力时 S=T
D = 模型宽度（d_model）
F = FFN 中间层宽度（d_ff），通常 F=4D
N = Query 头数
K = KV 头数（MHA 时 K=N，GQA 时 K<N）
H = 每个头的维度
L = 层数
V = 词表大小

关于门控 einsum：上图使用了”门控 FFN”，把一个大矩阵拆成两个，输出逐元素相乘作为门控。LLaMA、DeepSeek 等模型都用这种方式。如果不用门控，FFN 只有 2 个矩阵（2DF 参数），通常会把 D 或 F 放大来保持总参数量。

关于注意力变体：

MHA（多头注意力）：K=N
MQA（多查询注意力）：K=1
GQA（分组查询注意力）：1<K<N

MLP（前馈网络）

门控 FFN 有 3 个矩阵乘法：

操作	训练 FLOPs	参数量
输入 × W_in1 [D→F]	6BTDF	DF
输入 × W_in2 [D→F]	6BTDF	DF
门控 + 激活（逐元素）	~0	-
中间层 × W_out [F→D]	6BTDF	DF
合计	18BTDF	3DF

注意力层

QKVO 四个投影矩阵：

操作	训练 FLOPs	参数量
Q 投影 [D → N×H]	6BTDNH	DNH
K 投影 [D → K×H]	6BTDKH	DKH
V 投影 [D → K×H]	6BTDKH	DKH
O 投影 [N×H → D]	6BTDNH	DNH
合计	12BTD(N+K)H	2D(N+K)H

点积注意力（Q·K 和 Attn·V）：

操作	训练 FLOPs
Q[B,T,K,G,H] · K[B,S,K,H]	6BTSNH
softmax（逐元素）	~0
Attn[B,T,S,K,G] · V[B,S,K,H]	6BTSNH
合计	12BT²NH（自注意力 S=T）

因果掩码：如果用因果掩码（只看前面的 token），实际 FLOPs 减半。需要用注意力 kernel 而不是朴素 einsum 才能实现这个优化。

其他操作

操作	训练 FLOPs	参数量
LayerNorm	~0	~D
解嵌入 [D → V]（只算一次）	6BTDV	DV

参数和 FLOPs 总览

忽略注意力 softmax 的情况下，每层总 FLOPs：

\[18BTDF + 12BTD(N+K)H\]

如果 F=4D，D=NH，K=N（MHA），简化为：

\[18BT \cdot 4D^2 + 24BTD^2 = 96BTD^2\]

总参数约为 $3DF + 4D^2 = 16D^2$

所以：

\[\text{每层 FLOPs} = 6 \times BT \times \text{参数量}\]

这就是 6 × token 数 × 参数量 公式！

注意力什么时候开始贵？

点积注意力是 $O(T^2)$，矩阵乘法是 $O(T)$。什么时候注意力开始主导？

\[\frac{\text{注意力 FLOPs}}{\text{矩阵乘法 FLOPs}} = \frac{12BT^2NH}{96BTD^2} = \frac{T}{8D}\]

当 T > 8D 时，注意力 FLOPs 开始主导。

对于 D=8192 的大模型，这是 64K token。所以对于大模型，注意力的二次成本其实没那么可怕。

对于小模型（如 D=4608 的 Gemma-27B），约 32K 时注意力就开始主导了。

一些进阶话题

混合专家模型（MoE）

MoE 把一个大 FFN 换成 E 个小 FFN（”专家”），每个 token 只激活其中 k 个。

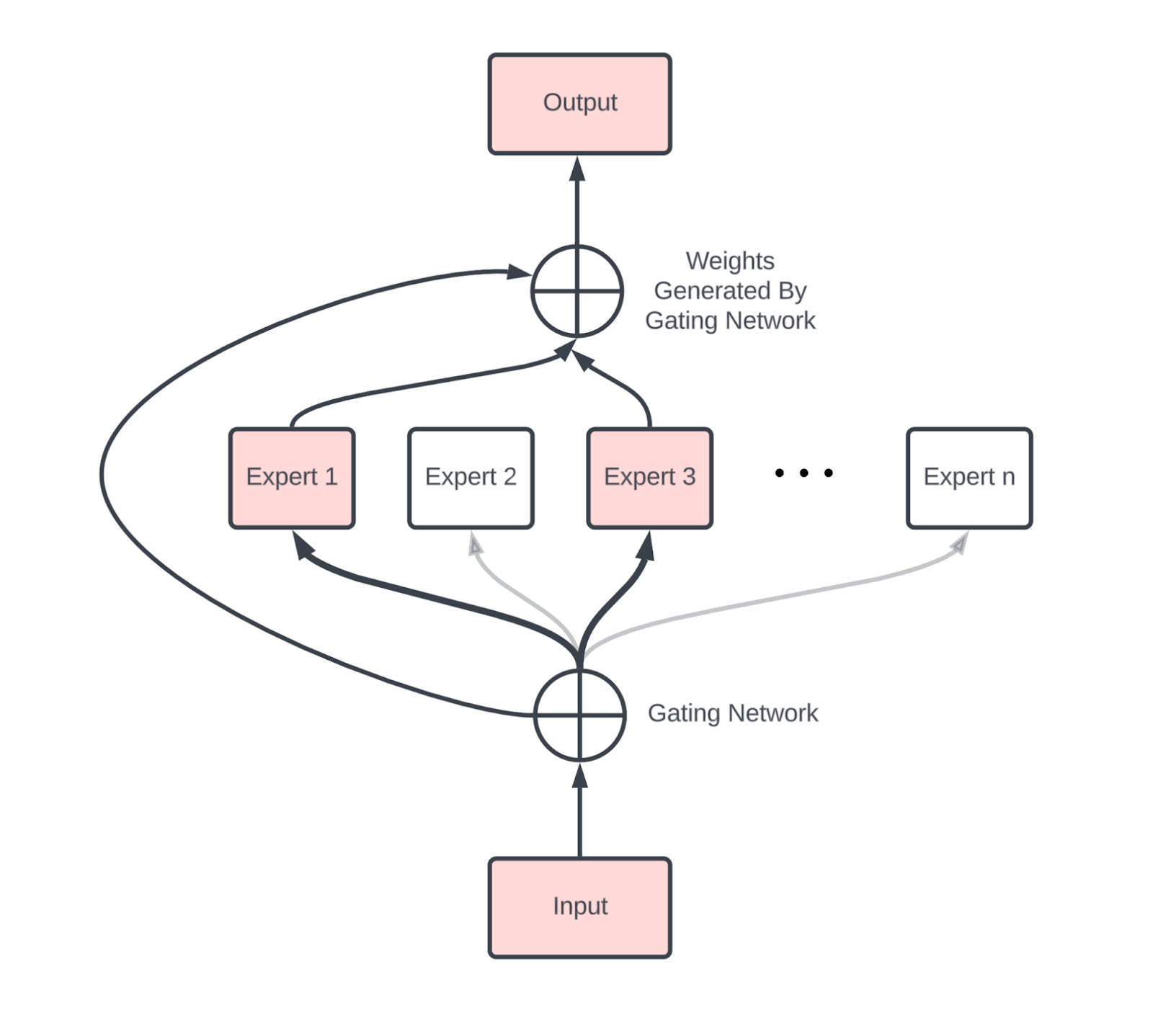
**MoE 层**：n 个专家，每个 token 路由到 k 个。参数量是 n 倍，但每个 token 只用 k 个。来源。

参数量：增加 E 倍
每 token FLOPs：增加 k 倍
稀疏度 E/k：通常 8-64（如 DeepSeek v3 用 E=256, k=8）

MoE 引入的通信开销主要是两次 AllToAll——把 token 发到对应专家所在的设备，再发回来。严格说只有数据/序列分片和专家分片同轴时才需要。好消息是 AllToAll 只有 AllGather 成本的 1/4。

梯度检查点（重计算）

反向传播需要保存前向传播的中间结果。一个 B×T=4M、L=64、D=8192 的模型，完整保存需要约 84TB 激活值！

为什么这么多？ Transformer 每层约有 20 个中间结果需要保存（每个矩阵乘法的输入输出、激活函数的输入输出等）。

解决办法：梯度检查点（gradient checkpointing / rematerialization）

两种常见策略：

激进重计算：只保存每层输入，反向时重新算一遍前向。内存降到 1/20，FLOPs 从 6ND 增加到约 8ND。
只保存大矩阵乘法输出：保存 7 个矩阵乘法的输出（QKVO + 3个 FFN），避免重算它们，但激活函数等还是要重算。内存降到 7/20。

JAX 中用 jax.remat / jax.checkpoint 控制。

KV 缓存

推理分两个阶段：

预填充（Prefill）：处理用户输入，生成 KV 缓存
生成（Decode）：用 KV 缓存一个个生成 token

KV 缓存的形状是 $[2, S, L, K, H]$（2 是 K 和 V）。

有多大？ 以 int8 为例，8K 上下文、64 层、D=8192：

\[2 \times 8192 \times 64 \times 8192 = \textbf{8GB}\]

每个请求 8GB！ 这就是为什么 GQA（减少 K）很重要——KV 头数少了，缓存就小了。

本章小结

组件	每层参数量	每层训练 FLOPs
MLP	3DF	18BTDF
注意力	2D(N+K)H	12BTD(N+K)H + 12BT²NH
LayerNorm	~D	~BTD
词嵌入（总计）	DV	12BTDV

几个记忆点：

MLP 占大头参数，只要 T < 8D，也占大头 FLOPs
训练 FLOPs ≈ 6 × 参数量 × token 数
KV 缓存 ≈ 2 × S × L × K × H 字节

练习题

题 1：一个模型 D=4096, F=4D, V=32000, L=64。多少参数？注意力参数占比？每 token KV 缓存多大？（假设 MHA，N×H=D，int8 KV）

答案

参数 = L × (3DF + 4D² + D) + 2DV = 64 × (3×4K×16K + 4×16M + 4K) + 2×4K×32K ≈ 16B（160亿）
注意力占比 = 4D² / (4D² + 3DF) = 4D² / (4D² + 12D²) = 1/4
KV 缓存 = 2 × L × D = 2 × 64 × 4096 = 512KB/token

题 2：在 {'X':4, 'Y':8, 'Z':4} 网格上执行 A[B_X, D_Y] · W[D_Y, F] → C[B_X, F]，总 FLOPs 是多少？每卡 FLOPs 是多少？

答案

理论总 FLOPs = 2BDF
但 Z 轴没用，实际做了 Z 份重复计算 → 实际 = 2BDF × Z
每卡 = 2BDF / (X×Y)

题 3：A[I,J,K,L] · B[I,J,M,N,O] → C[K,L,M,N,O] 的 FLOPs？

答案

I, J 是收缩维度，K,L,M,N,O 是非收缩维度，没有批次维度。

FLOPs = 2 × I × J × K × L × M × N × O

题 4：自注意力（不含 QKVO 投影）的算术强度是多少？在什么上下文长度时是计算受限的？

答案

用 Flash Attention 的话：

加载：Q + K + V = 4BTNH + 4BSKH 字节
FLOPs：4BTSNH（Q·K 和 Attn·V）

强度 = FLOPs / 字节 = 4BTSKGH / (4BHK(TG+S))

预填充/训练（S=T）：强度 ≈ T（线性增长）→ T > 240 时计算受限

生成（T=1）：强度 ≈ G（组大小）→ 基本总是内存受限

题 5：自注意力 FLOPs = QKVO 投影 FLOPs 时，序列长度是多少？

答案

24BTDNH = 12BT²NH → T = 2D

对于 D=4096，T = 8192。说明大多数情况下矩阵乘法 FLOPs 更大。

题 6：如果只保存 7 个大矩阵乘法的输出（QKVO + 3个 FFN），反向传播需要重算多少额外 FLOPs？

答案

需要重算两个注意力矩阵乘法（Q·K 和 softmax·V）：

额外 FLOPs = 4BT²NH

其他重算的操作都是 O(BTD)，可忽略。

题 7：DeepSeek v3 声称用 2.79M H800 小时训练了 14.8T token，激活参数 370 亿。硬件利用率是多少？（提示：FP8 无稀疏性）

答案

H800 FP8 无稀疏：~1.5×10¹⁵ FLOPs/s
总可用 = 2.79×10⁶ × 1.5×10¹⁵ × 3600 = 1.5×10²⁵ FLOPs
理论需要 = 6 × 37×10⁹ × 14.8×10¹² = 3.3×10²⁴ FLOPs
利用率 = 3.3×10²⁴ / 1.5×10²⁵ ≈ 22%

题 8：MoE 有 E 个专家，每 token 激活 k 个。在 TPU v5e 上用 int8 权重，需要多大 batch 才能计算受限？DeepSeek（E=256, k=8）呢？

答案

加载：E × D × F 字节
FLOPs：2 × k × B × D × F

强度 = 2kBDF / (EDF) = 2kB/E

计算受限：2kB/E > 240 → B > 120E/k

DeepSeek：B > 120 × 256 / 8 = 3840 token

生成时这是个很大的 batch！

第 4 章完！下一章讲 Transformer 训练并行化，点击继续。

附录

附录 A：Flash Attention 原理

传统反对长上下文的理由是：注意力 FLOPs 和内存都是 $O(T^2)$。但有两个重要反驳：

FLOPs 其实没那么可怕：只有 T > 8D 时注意力才主导，而且单次注意力的内存相对于所有权重和激活来说很小。
不需要生成完整的 T×T 矩阵！ 用局部计算和累积统计量，可以实现常数内存的注意力。

第二点就是 Flash Attention 的核心思想。

基本做法：按 K/V 的块来计算注意力，维护三个运行统计量：

M：运行最大值 max(Q·K)
L：运行分母 Σexp(Q·K - M)
O：运行输出

每处理一个块，就用新块的统计量更新这三个值。关键公式：

\[L^\text{new} = e^{M^{old} - M^{new}} \cdot L^{old} + e^{M^{cur} - M^{new}} \cdot L^{cur}\]

硬件视角：把 Q 块放进 VMEM（片上高速内存），每次迭代只加载 KV 块，提高算术强度。运行统计量也留在 VMEM 中。

反向传播的技巧：注意力 softmax 有一个巧妙的恒等式，可以把沿序列长度的归约变成沿特征维度的归约：

\[S \cdot_j dS = dO \cdot_d O\]

这让反向传播也能分块计算，还使得环形注意力等更高级的分片方案成为可能。

Miscellaneous

^*Work done at Google DeepMind, now at MatX.

Citation

For attribution in academic contexts, please cite this work as:

    Austin et al., "How to Scale Your Model", Google DeepMind, online, 2025.

or as a BibTeX entry:

    @article{scaling-book,
      title = {How to Scale Your Model},
      author = {Austin, Jacob and Douglas, Sholto and Frostig, Roy and Levskaya, Anselm and Chen, Charlie and Vikram, Sharad
      and Lebron, Federico and Choy, Peter and Ramasesh, Vinay and Webson, Albert and Pope, Reiner},
      publisher = {Google DeepMind},
      howpublished = {Online},
      note = {Retrieved from https://jax-ml.github.io/scaling-book/},
      year = {2025}
    }